유클리드 호제법

유클리드 호제법이란

• 두 양의 정수 혹은 두 다항식의 최대 공약수를 구하는 방법이다.
• 호제법이란 두 수가 서로 상대방 수를 나누어 결국 원하는 수를 얻는 알고리즘을 말한다.

 

알고리즘

• 두 양의 정수 a, b (a > b)에 대하여 a를 b로 나눈 나머지를 r이라 하면, a, b의 최대 공약수는 b와 r의 최대 공약수와 같다.
• 이 성질에 따라 b를 r로 나눈 나머지 r'를 구하고 다시 r을 r'로 나눈 나머지를 구하는 과정을 반복하여 나머지가 0이 되었을 때 나누는 수가 a와 b의 최대공약수이다.

 

 

 

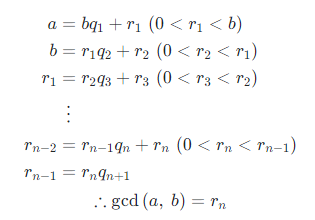
Ex) 78696, 19332의 최대 공약수를 구하시오.

78696 = 19332 x 4 + 1368

19332 = 1368 x 14 + 180

1368 = 180 x 7 + 108

180 = 108 x 1 + 72

108 = 72 x 1 + 36

72 = 36 x 2 + 0

 

최대공약수는 36

• 78696를 19332로 나누면 몫은 4 나머지는 1368이다.
• 나눈 19332를 나머지 1368로 나누면 몫은 14 나머지는 180이다.
• 나눈 1368을 나머지 180으로 나누면 몫은 7 나머지는 108이다.
• 이과정을 반복하면, 나눈 72를 나머지 36으로 나누었을 때 나머지가 0이 나온다.
• 즉, 나머지 0이 나왔을 때 나누었던 수인 36이 최대공약수이다.

 

그럼 만약 a가 0이거나 b가 0이면?

• a가 0이면 b가 최대공약수이고, b가 0이면 a가 최대공약수이다.

Ex) 0, 11의 최대공약수는 11

 

 

 

최소공배수

• 최소 공배수는 서로 다른 수 a, b의 배수 중에서 공통되는 배수 중에 가장 작은 값을 의미한다.
• a, b의 곱을 a, b의 최대 공약수로 나누면 구할 수 있다.

a, b의 최소 공배수 = a * b ÷ a, b의 최대공배수

 

---

 

Python

최대 공약수

def gcd(a, b):
    while b > 0:
        a, b = b, a % b
    return a

• while문을 통해 b가 0보다 크면 계속 반복된다.
• b를 a에 a와 b를 나눈 값을 b에 대입하여 b가 0이 될 때까지 반복한다.
• b가 0이 되었을 때 나눈 값 인 a를 return한다.

 

최소 공배수

def lcm(a, b):
    return a * b // gcd(a, b)

• 위에서 구한 최대 공약수를 토대로 최소 공배수를 구한다.
• a와 b를 곱한 값에 a와 b의 최대 공약수를 나눈다.